【学习笔记】数学建模（未更完）

数学建模的一般步骤

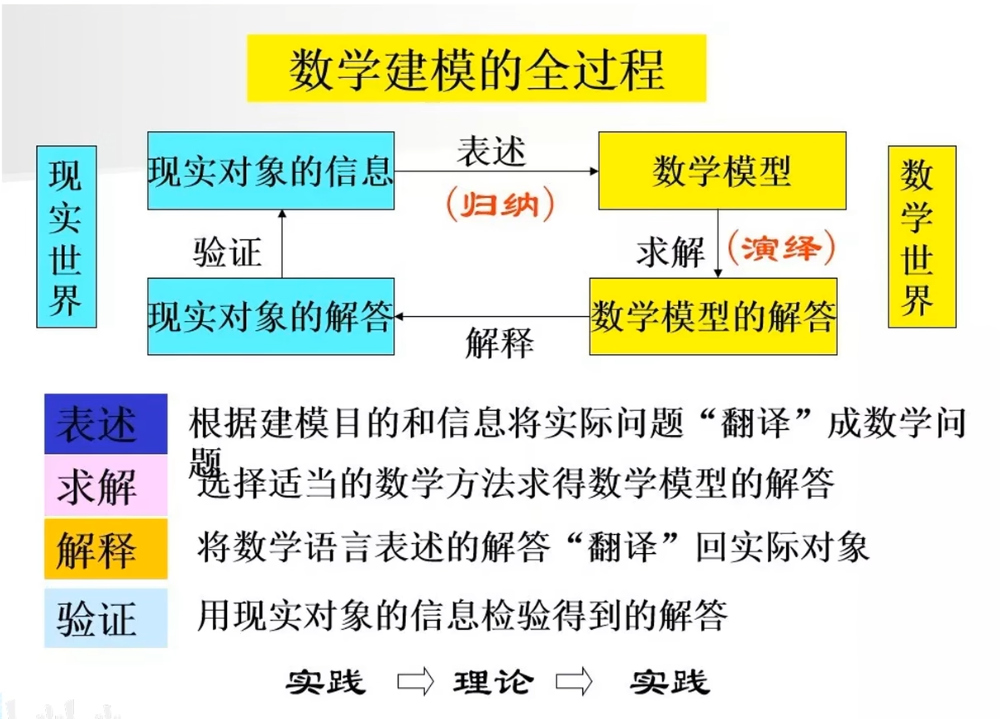
模型准备

了解问题的实际背景，明确其实际意义，掌握对象的各种信息。以数学思路来解释问题的精髓

模型假设

针对问题特点和建模目的作出合理的、简化的假设（在合理与简化之间作出折中）

建立模型

用数学的语言、符号描述问题，发挥想象力（尽量采用简单的数学工具）

模型求解

利用获取的数据资料，对模型的所有参数做出计算。推到模型的公式，将数学表达式变形为建模方法的标准形式，通过限制条件，对这个模型进行求解。

模型分析

对所要建立模型的思路进行阐述，对所得的结果进行数学上的分析。包括误差分析、数据稳定性分析等。

模型检验

用非技术性的语言回答实际问题。将模型分析结果与实际情形进行比较，以此来验证模型的准确性、合理性和适用性。

如果模型与实际较吻合，则要对结果给出其实际含义，并进行解释。
如果模型与实际吻合较差，则应该修改假设，再次重复建模过程。

论文要素

题目：
摘要、关键词：很重要
问题重述：用自己的语言对问题进行描述
问题假设：
问题分析
符号说明
模型建立
模型求解：使用编程语言求解（matlab、python、R等）
模型优缺点评价
参考文献

备战建模比赛

分工协作及对应要求

建模员

需要系统掌握各类模型，做到

模型功能
模型适用场景
实现该模型需要的条件
模型有哪些缺点或不足，可以做出哪些改进

学习基础知识->学习算法知识->学习优秀论文

程序员

需要掌握Matlab/Python，做到

熟练掌握编程基础
实现各类常见算法
对程序Bug做出改正
熟练利用编程或软件制作精美图片

学习编程知识->调试常用模型->复现优秀论文

写作员

需要熟练撰写论文各模块内容

掌握学术语言规范
明白论文各模块写作要求
能够对论文进行排版
若撰写英文论文，需要能翻译并检查论文错误

掌握写作要求->掌握学术语言->掌握排版技巧

赛题类型

一、预测类

解题一般步骤：

确定预测目标
收集、分析资料
选择合适的预测方法预测
分析评价预测方法及其结果
修正预测结果
给出预测结果

方法选择

小样本内部预测：插值与拟合方法中、大样本内部预测：回归分析法小样本的未来预测：灰色预测方法中、大样本的随机因素或周期特征的未来预测：时间序列方法大、特大样本未来预测：神经网络方法

二、评价类

解题一般步骤

明确评价目的
确定被评价对象
建立评价指标体系
确定各指标相对应的权重系数
选择或构造综合评价模型
计算各系统的综合评价值
给出综合评价结果

三、机理分析类

四、优化类

解题一般步骤

确定优化目标
确定决策变量
构建目标函数
根据已知条件构建约束条件
选择合适的方法求解目标函数
给出优化结果

模型

线性规划模型

有限的条件下，最大的收益

例题：张麻子既要攻碉楼又要追替身，他们一伙6人，总共1200发子弹；每有一人攻碉楼会给百姓带来40点士气值，每有一人追替身会给百姓带来30点士气值；攻碉楼每人需240发子弹，追替身每人需120发。问攻碉楼和追替身各派几个人，能使百姓的士气值最大？

解：设x₁人攻碉楼，x₂人追替身，百姓士气值为y；士气值最大：max y = 40x₁ + 30x₂；总共6人：x₁ + x₂ = 6；子弹有限：240x₁ + 120x₂ ≤ 1200；既要攻碉楼又要追替身：x₁ ≥ 1 ， x₂ ≥ 1；

适用经典赛题

题目中提到“怎样安排/分配”、“尽量多(少)”、“最多(少)"、"利润最大"、最合理等
生产安排：原材料、设备有限制，总利润最大
投资收益：资产配置、收益率、损失率、组合投资、总收益最大而不是总收益率
销售运输：产地、销地、产量、销量、运费，总运费最省
车辆安排：路线、起点终点、承载量、时间点、车次安排最合理
整数规划、0-1规划

代码实现

模型化matlab标准型：目标函数最小值、约束条件小于等于或等号
如果有最大值怎么办？约束条件有大于等于怎么办？
- 式子两边加负号

变量名	含义
f	目标函数的系数列向量
A,b	不等式约束条件的变量系数矩阵和常数项矩阵
Aeq,beq	等式约束条件的系数矩阵和常数项矩阵
lb,ub	决策变量的最小取值和最大取值

[x,fval] = linprog(f,A,b,Aeq,beq,lb,ub)
x返回最优解的变量取值，fval返回目标函数的最优值
若不存在不等式约束，用”[]“代替A和b
若不存在等式约束，用”[]“代替Aeq和beq
没有等式约束和最小、最大取值的约束时，可以不写Aeq,beq,lb,ub：[x,fval] =linprog(f,A,b)

f = [-40;-30]; %目标函数中变量的系数矩阵
a = [1,1;-1,0;0,-1;240,120]; %小于等于的约束条件中系数矩阵
b = [6;-1;-1;1200]; %小于等于的约束条件中常数项矩阵


[x,y] = linprog(f,a,b);
y=-y;

非线性规划模型

有限的条件下，最大的收益

至少一个变量不是一次方

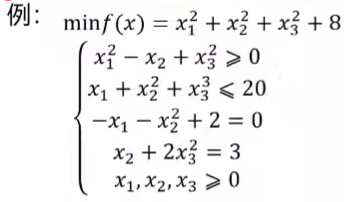
变量名	含义
fun	单独函数文件里定义的目标函数
x0	决策变量的初始值。不知道就随便写个数
A,b	不等式约束条件的变量系数矩阵和常数项矩阵（都是<=）
Aeq,beq	等式约束条件的系数矩阵和常数项矩阵
lb,ub	决策变量的最小取值和最大取值
nonlcon	非线性约束，包括不等式和等式

[x,fval] = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)
x得到决策变量取值，fval得到最优解取值

本题： [x,y] = fmincon('fun1',[0;0;0],[],[],[],[],[0;0;0],[],'fun2')

1
2
3

%% fun1 目标函数
function f = fun1(x)
f = sum(x.^2) + 8;

%% fun2 非线性约束
function [g,h] = fun2(x)
g = [-x(1)^2+x(2)-x(3)^2 
x(1)+x(2)^2+x(3)^3-20] % g是非线性不等式
h = [-x(1)-x(2)^2+2
x(2)+2*x(3)^2-3]

适用经典赛题
- 题目中提到“怎样安排/分配” ...
- 投资规划：资产配置、收益率、损失率、组合投资、总收益率最大
- 角度调整：飞行管理避免相撞；影院最佳视角

多目标规划模型

既要XXX，又要XXX

需要衡量每个目标的完成情况，并在主观上区分三个目标的重要性，使得整体完成情况尽量好

引入三个概念：正负偏差变量、绝对约束和目标约束、优先因子
衡量每个目标的完成情况：正负偏差变量

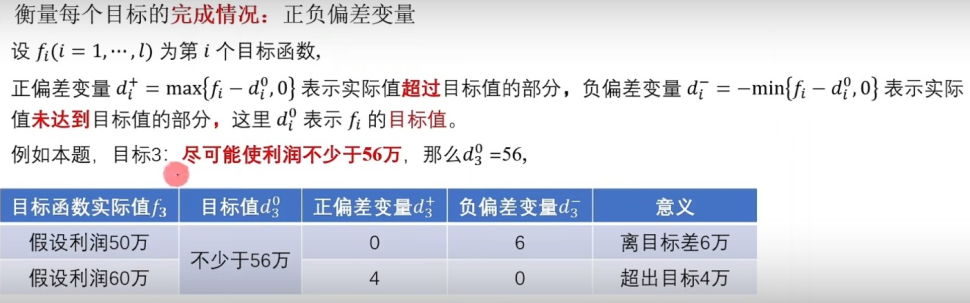
层次分析法基本模型（AHP）

三大典型应用

最佳方案的选取（选择运动员、选择地址）
评价类问题（评价水质状况、评价环境）
指标体系的优选（兼顾科学和效率）

步骤

建立层次结构模型

最高层：决策的目的、要解决的问题

最低层：决策时的备选方案

中间层：考虑的因素、决策的准则

对于相邻的两层，称高层为目标层、低层为因素层
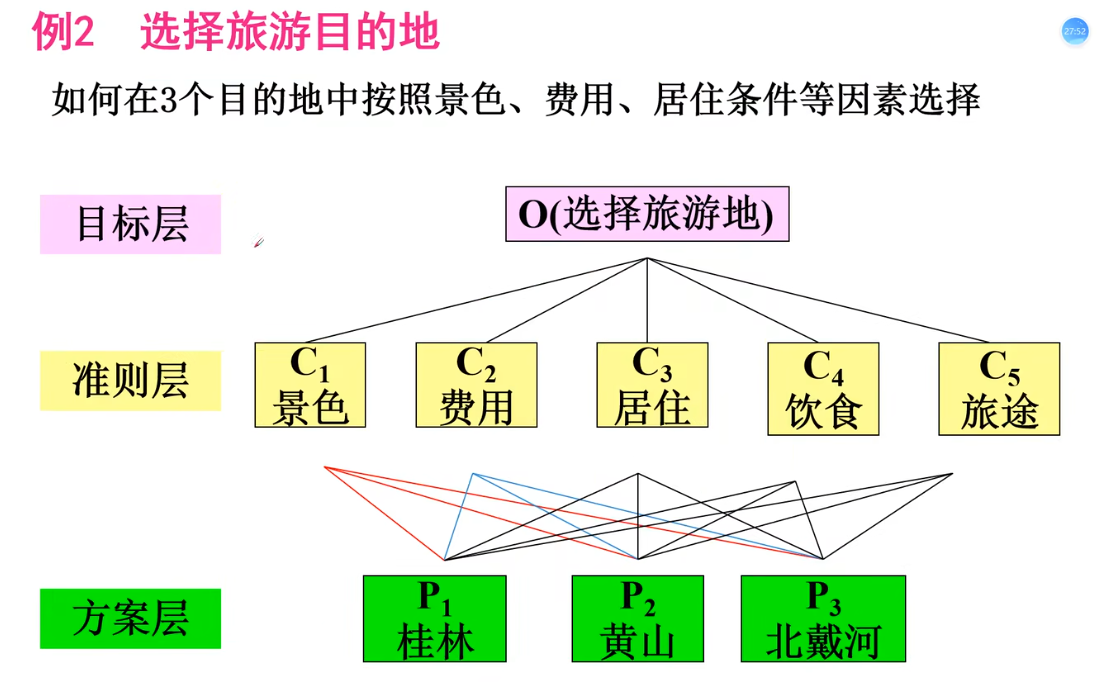
构造判断（成对比较）矩阵
1. 不把所有因素放在一起比较，而是两两相互比较
2. 对此时采用相对尺度，以尽可能减少性质不同的的因素比较的困难，以提高准确度
  
  设要比较各准则C₁、C₂、C₃、C₄、C₅对目标O的重要性 C_i : C_j = a_ij
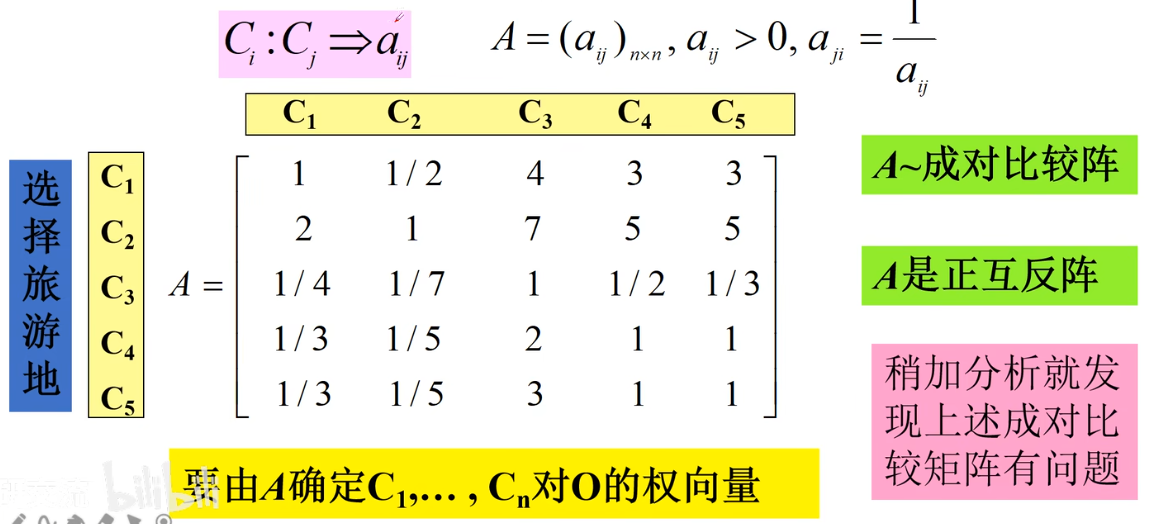
  - 对角线元素一定为1
  - a_ij = 1/a_ji
  上述矩阵存在不一致问题，允许不一致，但要确定不一致的范围
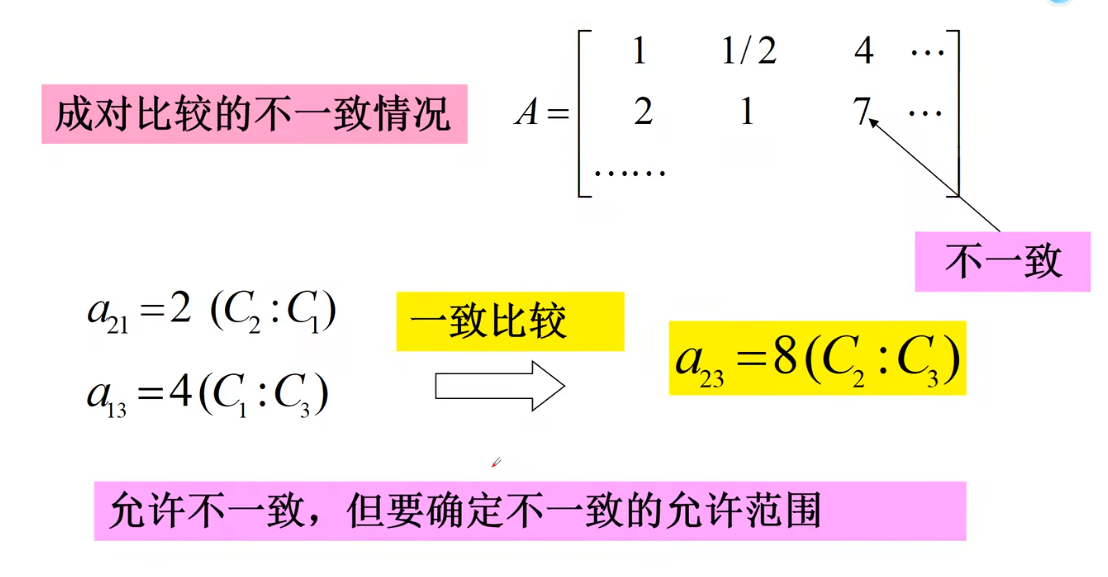
层次单排序及其一致性检验
1. 对应于判断矩阵的最大特征根λ_max的特征向量，经归一化后记为W
2. W的元素为同一层次因素对于上一层次因素某因素相对重要性排序权值，这一过程称为层次单排序
能否确认层次单排序，需要进行一致性检验，指对A确定不一致的允许范围

定理：n阶一致阵的唯一非零特征根为n

定理：n阶正互反阵A的最大特征根λ≥n，当且仅当λ=n时A为一致阵

定义一致性指标： \[ {CI} CI=\frac{\lambda-n}{n-1} \] {一致性指标} CI=0，有完全的一致性 CI接近于0，有满意的一致性 CI越大，不一致越严重
层次总排序及其一致性检验

MATLAB

基操

clear %清空工作区
clc %清空控制台
disp(str); %输出str信息
A = input('请输入矩阵A');
size(A);

矩阵

B = A' %求A的转置矩阵
[D,V] = eig(A)； %求特征值和特征向量
E = inv(A); %求逆矩阵
C = A*B; %矩阵乘法
E = A.*B; %矩阵点乘，对应元素相乘

作图

二维图

线图

plot函数用来创建x和y的简单线图

x = 0:0.05:30 %从0到30，每隔0.05取一次值
y = sin(x);
plot(x,y); %若(x,y,'LineWidth',2)可让函数曲线变粗
xlabel('横轴标题');
ylabel('纵轴标题');
grid on %显示网格
axis([-5 35 -2 2]);

条形图

bar函数创建垂直条形图 barh函数创建水平条形图

t = -3:0.5:3;
p = exp(-t.*t);
bar(t,p);
barh(t,p);

极坐标图

polarplot函数用来绘制极坐标图

theta = 0:0.01:2*pi;
% abs求绝对值或复数的模
radi = abs(sin(2*theta).*cos(2*theta));
polarplot(theta,radi); %括号内是弧度和半径

散点图

scatter函数用来绘制x和y的散点图

Height = randn(1000,1);
Weight = randn(1000,1);
scatter(Height,Weight);
xlabel('Height');
ylabel('Weight');

三维图和子图

三位曲面图

surf函数可以用来做三维曲面图。一般是展示函数z=z(x,y)的图像。

首先需要用meshgrid创建好空间上(x,y)点。

[X,Y] = meshgrid(-2:0.2:2);
%Z = X.^2 + Y.^2;
Z = X.*exp(-X.^2 - Y.^2;);
surf(X,Y,Z);

colormap spring % colormap设置颜色，可跟winter、summer、hsv
colorbar

子图

使用subplot函数可以在同一窗口的不同区域显示多个绘图

theta = 0:0.01:2*pi;
radi = abs(sin(2*theta)*cos(2*theta));
Height = randn(1000,1);
Weight = randn(1000,1);

subplot(2,1,1); surf(X.^2); title('1st');
subplot(2,1,2); surf(Y.^2); title('2nd');

处理缺失/异常值

使用实时脚本文件，任务——清理缺失数据/清理离群数据

x = 1:100; %构造一个数组，元素为1,2,3,...,100
% randn(1,100)意味着生成一个1行100列的矩阵
% 矩阵元素的均值为0，方差σ^2=1，且是正态分布的随机数
data = randn(1,100);

data(20:20:80) = NaN;

data(10) = -50;
data(40) = 45;
data(70) = -20;
data(90) = 20;
plot(x,data);

搜索技巧

完全匹配搜索

查询词的外边加上双引号“”

引号中英文均可
例如搜索 “CT参数标定” ，则搜索结果不是分别带有“CT”或“参数标定”的网页

标题关键词搜索

查询词的前边加上intitle:

冒号为英文冒号
例如搜索 intitle:CT参数标定，则搜索结果每一个标题都带有“CT参数标定”

搜索文档

查询词后空格再输入filetype:文件格式(doc/pdf/xls/等)

例如搜索线性规划 filetype:pdf ，则搜索结果都是pdf的资料

去掉不想要的

查询词后边加空格后加减号关键字

例如搜索线性规划 filetype:pdf -百度文库

查文献

知网

优先查看知网的硕博士论文

谷歌学术

国内无法访问，可访问谷歌学术镜像

查数据

国家统计局

GitHub项目

GitHub上的一个项目，包含了经济、地理、能源、教育等所有你能想到的领域的数据
https://github.com/awesomedata/awesome-public-datasets

数据预处理

缺失值

比赛提供的数据，发现有些单元格是null或空
缺失太多直接将该项删除
最简单的处理：均值、众数插补
- 定量数据：例如身高年龄等，用整体的均值来补缺失
- 定性数据：例如性别文化程度等，用众数来补缺失
- 使用赛题：人口的数量年龄、经济产业情况等统计数据，对个体精度要求不大的数据
Newton插值法
- 根据固定公式，构造近似函数，补上缺失值，普遍适用性强
- 缺点：区间边缘处的不稳定震荡，即龙格现象。不适合对导数有要求的题目
- 使用赛题：热力学温度、地形测量、定位等只追求函数值而不关心变化的数据
样条插值法
- 用分段光滑的曲线去插值，光滑意味着曲线不仅连续，还要有连续的曲率
- 使用赛题：零件加工、水库水流量、图像“基线漂移”、机器人轨迹等精度要求高、没有突变的数据

异常值

样本中明显和其他数值差异很大的数据
正态分布3σ原则
- 数值分布在(μ-3σ,μ+3σ)中的概率为99.73%，其中μ为平均值，σ为标准差
- 求解步骤：
  1. 计算均值μ和标准差σ
  2. 判断每个数据值是否存在(μ-3σ,μ+3σ)内，不在则为异常值
- 适用题目：总体符合正态分布，例如人口数据、测量误差、生产加工质量、考试成绩等
- 不适用题目：总体符合其他分布，例如公交站人数排队论符合泊松分布
画箱型图
- 箱型图中，把数据从小到大排序。下四分位数Q1是排第25%的数值，上四分位数Q3是拍第75%的数值
- 四分位距IQR=Q3-Q1，也就是排名第75%的减去第25%的数值
- 与正态分布类似，设置个合理区间，在区间外的就是异常值
- 一般设[Q1-1.5×IQR，Q3+1.5×IQR]